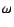 is expressed as
is expressed as
The dispersion relation at wavenumber 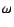 is expressed as
is expressed as
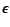 ( (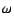 ) = ) = 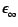 + + 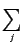 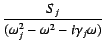
|
(1) |
where
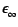 is the dielectric constant representing
the contribution from higher wavenumber,
Sj,
is the dielectric constant representing
the contribution from higher wavenumber,
Sj,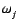 ,
,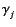 are the oscillator strength,
resonant wavenumber, and damping factor, respectively.
are the oscillator strength,
resonant wavenumber, and damping factor, respectively.
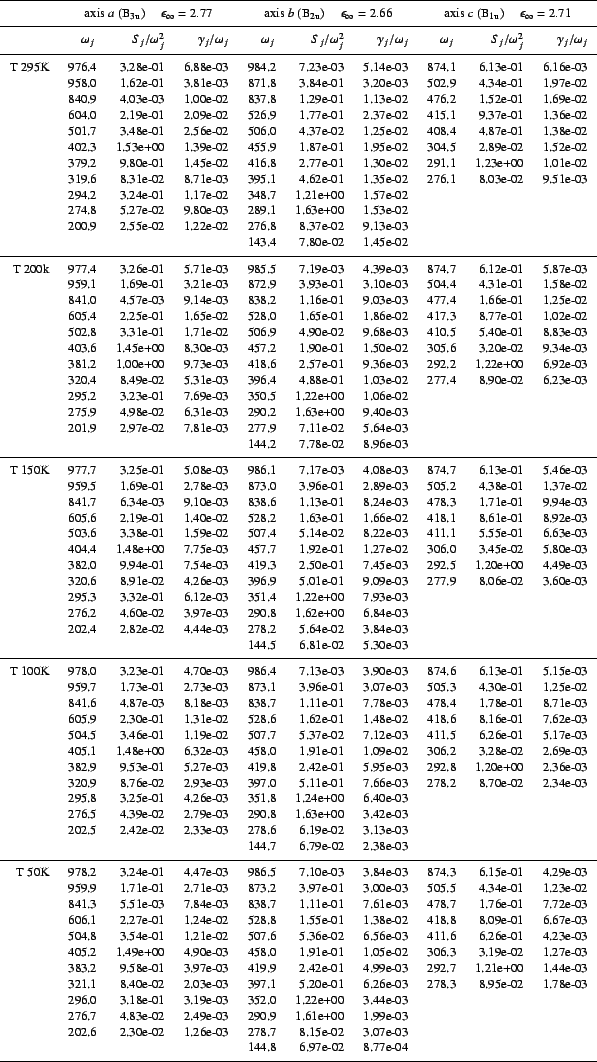
Table 1:
Forsterite oscillator parameters for temperatures from 295K to 50K.
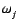 is in cm-1 and
Sj/
is in cm-1 and
Sj/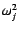 ,
,
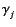 /
/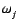 are non dimensional.
are non dimensional.