Infrared Spectra of Fayalite Crystal
H. Suto, C. Koike, H. Sogawa, Akira Tsuchiyama, H. Chihara, and K. Mizutani
Astronomy and Astrophysics, 389, 568-571, 2002

The dielectric constant for each axis is expressed in the oscillator model by a function of wavelength $\lambda$ as


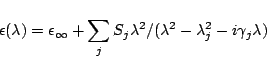\begin{displaymath} \epsilon (\lambda) = \epsilon_{\infty} + \sum_{j} S_j\lambda^{2} / (\lambda^2 - \lambda_j^2 -i \gamma_j \lambda) \end{displaymath} (1)

Here, $\epsilon_{\infty}$ is the dielectric constant at the short wavelength limit, $S_j, \lambda_j, \gamma_j$ are the oscillator strength, transverse optical wavelength, and dumping factor, respectively, and $i$ is the imaginary number unit.

Table 1: Peak positions and reflectivity of fayalite crystal and its oscillator parameters
//$c$ axis ($B_{1u}$) $\epsilon_{\infty} = 3.50$
$\lambda_{peak} \mu m$ $R_{peak}$ $\lambda_j$ $\gamma_j$ $S_j$
11.20 0.86 11.64 0.15 0.74
20.62 0.79 21.44 0.44 0.64
22.47 0.31 22.37 0.93 0.16
26.49 0.44 26.94 1.15 0.37
31.86 0.84 33.04 0.88 2.58
40.04 0.39 39.78 1.26 0.20
50.96 0.58 51.18 1.09 0.63
//$b$ axis ($B_{2u}$) $\epsilon_{\infty} = 3.35$
$\lambda_{peak} \mu m$ $R_{peak}$ $\lambda_j$ $\gamma_j$ $S_j$
10.54 0.55 10.62 0.06 0.029
11.33 0.86 11.65 0.09 0.39
12.09 0.47 12.10 0.09 0.12
19.49 0.63 19.98 0.41 0.24
21.34 0.46 21.48 0.66 0.40
29.21 0.54 30.11 1.10 0.14
33.89 0.85 36.76 1.29 2.25
39.21 0.60 39.30 1.10 0.98
55.31 0.63 55.82 1.31 0.79
58.26 0.47 58.13 1.42 0.30
//$a$ axis ($B_{3u}$) $\epsilon_{\infty} = 3.55$
$\lambda_{peak} \mu m$ $R_{peak}$ $\lambda_j$ $\gamma_j$ $S_j$
10.37 0.84 10.64 0.12 0.27
10.91 0.74 10.95 0.07 0.32
12.06 0.25 12.05 0.08 0.03
17.68 0.73 18.33 0.43 0.73
21.81 0.12 21.70 0.50 0.01
27.47 0.66 28.32 0.97 0.35
32.51 0.86 34.30 1.00 3.10
45.99 0.34 45.35 1.70 0.10
55.02 0.49 55.10 0.90 0.30
57.14 0.42 56.95 1.00 0.16

Text data of table 1.