Infrared reflection spectra of forsterite crystal
H. Sogawa, C. Koike, H. Chihara, H. Suto, S. Tachibana, A. Tsuchiyama, and T. Kozasa
Astronomy and Astrophysics, 451, 357-361, 2006
In the infrared wavelength region, we assumed that
the dielectric funtion of crystal is represented by the dispersion relation
with the multiple oscillator model, which is given as
where
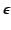 (
(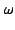 ) is a complex dielectric function
for the frequency
) is a complex dielectric function
for the frequency 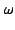 ,
,
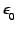 is the dielectric constant at the high-frequency limit, and
is the dielectric constant at the high-frequency limit, and
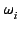 ,
,
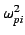 , and
, and 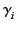 respectively represent the resonance frequency, the oscillator strength, and the damping constant of the i-th oscillator.
respectively represent the resonance frequency, the oscillator strength, and the damping constant of the i-th oscillator.
Table 1:
Oscillator Parameters for IR bands of forsterite crystal
B1u
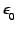 =2.71 =2.71 |
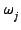 (cm-1) (cm-1) |
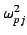 / /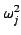 |
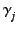 / /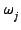 |
| 873.8 |
0.62 |
0.0058 |
| 502.2 |
0.45 |
0.021 |
| 476.3 |
0.16 |
0.017 |
| 415.1 |
1.02 |
0.015 |
| 408.4 |
0.42 |
0.013 |
| 304.5 |
0.026 |
0.014 |
| 291.2 |
1.26 |
0.011 |
| 276.1 |
0.074 |
0.0093 |
B2u
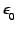 =2.66 =2.66 |
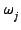 (cm-1) (cm-1) |
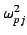 / /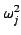 |
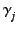 / /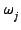 |
| 984.2 |
0.0071 |
0.0053 |
| 872.5 |
0.40 |
0.0055 |
| 838.8 |
0.11 |
0.0096 |
| 526.5 |
0.18 |
0.025 |
| 505.9 |
0.042 |
0.012 |
| 455.8 |
0.19 |
0.020 |
| 416.4 |
0.28 |
0.015 |
| 395.0 |
0.47 |
0.014 |
| 348.2 |
1.21 |
0.017 |
| 288.6 |
1.65 |
0.016 |
| 276.5 |
0.11 |
0.012 |
| 143.4 |
0.075 |
0.014 |
B3u
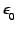 =2.77 =2.77 |
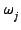 (cm-1) (cm-1) |
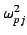 / /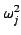 |
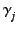 / /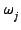 |
| 976.4 |
0.33 |
0.0064 |
| 957.9 |
0.17 |
0.0040 |
| 841.0 |
0.0029 |
0.0085 |
| 603.8 |
0.23 |
0.021 |
| 501.5 |
0.35 |
0.025 |
| 402.6 |
1.56 |
0.015 |
| 379.1 |
0.95 |
0.015 |
| 319.5 |
0.079 |
0.0084 |
| 294.0 |
0.32 |
0.012 |
| 274.6 |
0.054 |
0.011 |
| 200.8 |
0.027 |
0.014 |
Text data of table 1.
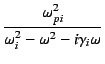 ,
,
![]() (
(![]() ) is a complex dielectric function
for the frequency
) is a complex dielectric function
for the frequency ![]() ,
,
![]() is the dielectric constant at the high-frequency limit, and
is the dielectric constant at the high-frequency limit, and
![]() ,
,
![]() , and
, and ![]() respectively represent the resonance frequency, the oscillator strength, and the damping constant of the i-th oscillator.
respectively represent the resonance frequency, the oscillator strength, and the damping constant of the i-th oscillator.